


Da Geometria Euclidiana à Geometria Fractal.
Projeto realizado no ano de 2014 na Escola Estadual Dimer Pizzetti com a turma de oitavo ano.
CONTEÚDOS
-
Razão e Semelhança.
-
Sequência.
-
Potenciação.
-
Noções primitivas; Ponto, Reta e Plano.
-
Infinito Absoluto e Infinito Potencial.
-
Medidas de Comprimento e de Área.
OBJETIVO GERAL
Estudar de forma dinâmica e unificada os conceitos matemáticos abordados neste projeto por meio da experimentação, análise e observação do concreto, concomitante à suas representações mais formais desenvolvidas em aula.
OBJETIVOS ESPECÍFICOS
-
Fazer uso de argumentos matemáticos para relatar as possíveis resoluções de uma situação-problema.
-
Perceber, em cada sequência de figuras, conceitos matemáticos que auxiliem na compreensão de padrões geométricos.
-
Desenvolver o pensamento abstrato criando e manipulando objetos concretos.
-
Incitar o aluno a perceber, pela observação e investigação, que entendimento dos conceitos matemáticos produzem uma melhor compreensão da realidade.
-
Aproximar o conhecimento matemático do convívio do aluno por meio da pesquisa e experimentação.
-
Exercitar os valores necessários para o bom êxito do trabalho em equipe; diálogo, respeito, participação, etc.
METODOLOGIA
Diário I) Observação e Aplicação.
Tempo: 60 min.
Atividade Proposta: Em grupos de quatro ou cinco integrantes, os alunos recebem uma sequência de figuras. A cada iteração, as figuras sofrem uma mudança se comparadas a sua versão anterior e, nessas mudanças, pode ser observado um padrão. É pedido aos alunos que registrem quais mudanças são visualmente percebidas e qual padrão havia na sequência apresentada. Além disso, pede-se que descubra uma relação entre a sequência de figuras e o conceito de potenciação (ambos já estudados em representações pictóricas de números quadrados e situações similares de sequência).
As imagens recebidas pelos alunos são bastante conhecidas:
Resultado: Os alunos apresentaram suas imagens e relataram os registros. Todos os grupos escreveram uma sequência de números em forma de uma potência e fizeram uma relação entre cada termo da sequência e as respectivas iterações observadas nas figuras.
Diário II) Referencial Teórico.
Tempo: 2 dias para leitura e formulação das perguntas; 90min de debate em aula.
Atividade Proposta: Leitura extra-classe do um artigo UMA PROPOSTA DIDÁTICA PARA O ENSINO DE GEOMETRIA FRACTAL EM SALA DE AULA NA EDUCAÇÃO BÁSICA pgs.(115 - 121)
Tópicos:
A Geometria Fractal
Características dos Fractais
Autossimilaridade
Complexidade Infinita ou Iteração
A Dimensão Fractal
Classificação dos Fractais
Após a leitura, formular duas perguntas para serem discutidas em sala.
Resultado: O tema foi apresentado e as perguntas formuladas foram respondidas conforme seguia a aula. Os alunos entenderam que já existiam estudos sobre as figuras que eles estavam analisando e que se tratavam de Fractais.
Para melhorar a compreensão do tema, conversamos sobre as três características que definem os fractais: a autossimilaridade, a complexidade infinita (iteração) e a dimensão fracionária.
Diário III) Pesquisa.
Tempo: 1 semana.
Atividade Proposta: Na internet, a pesquisa é feita nos sites selecionados com objetivo de responder uma lista de perguntas sobre a sequência de imagens recebida. Esta contém perguntas sobre o autor da imagem e sobre a própria imagem, enriquecendo o conceito matemático nela presente. As respostas ajudarão a compor o texto final do trabalho.
Resultado: Alguns grupos não encontraram todas as respostas e um grupo não pesquisou. As dúvidas das questões que não foram respondidas, posteriormente, buscamos sanar em encontros que aconteceram extra-classe com cada grupo.
Diário IV) Produção Textual.
Tempo: 1 hora por grupo.
Atividade Proposta: Com as respostas do questionário em mãos, será elaborado um texto que se refere ao tema recebido pelo grupo.
Resultado: Em horário extra-classe, reuni-me com cada grupo e juntos elaboramos os textos. Nesta etapa do trabalho os grupos estavam mais familiarizados com a atividade e puderam sanar algumas dúvidas conceituais que ainda eram presentes. Alguns foram entender mesmo o conceito de potenciação ou fractais depois de formularem o texto e iniciaram a parte prática.
Diário V) Trabalho Prático.
Tempo: 2 semanas.
Atividade Proposta: Cada grupo realiza em horário extra-classe, alguns na própria escola, a atividade pré definida de construção prática de um objeto relacionado ao seu tema estudado.
Resultado: Como a maior parte dos trabalhos foram criados a partir de objetos que já foram desenvolvidos por outros estudantes e cujos vídeos estão disponibilizados na rede, a dificuldade foi menor. Essa etapa do trabalho foi muito rica, principalmente pelo fato de trabalhar a matemática com algo diferente dos registros em papel.
Diário VI) Apresentação.
Tempo: 90 min.
Atividade Proposta: Cada aluno recebe, via e-mail, cópias de todos os textos feitos pelos grupos. O texto de seu grupo deve ser estudado para posterior apresentação em sala, juntamente com os objetos produzidos.
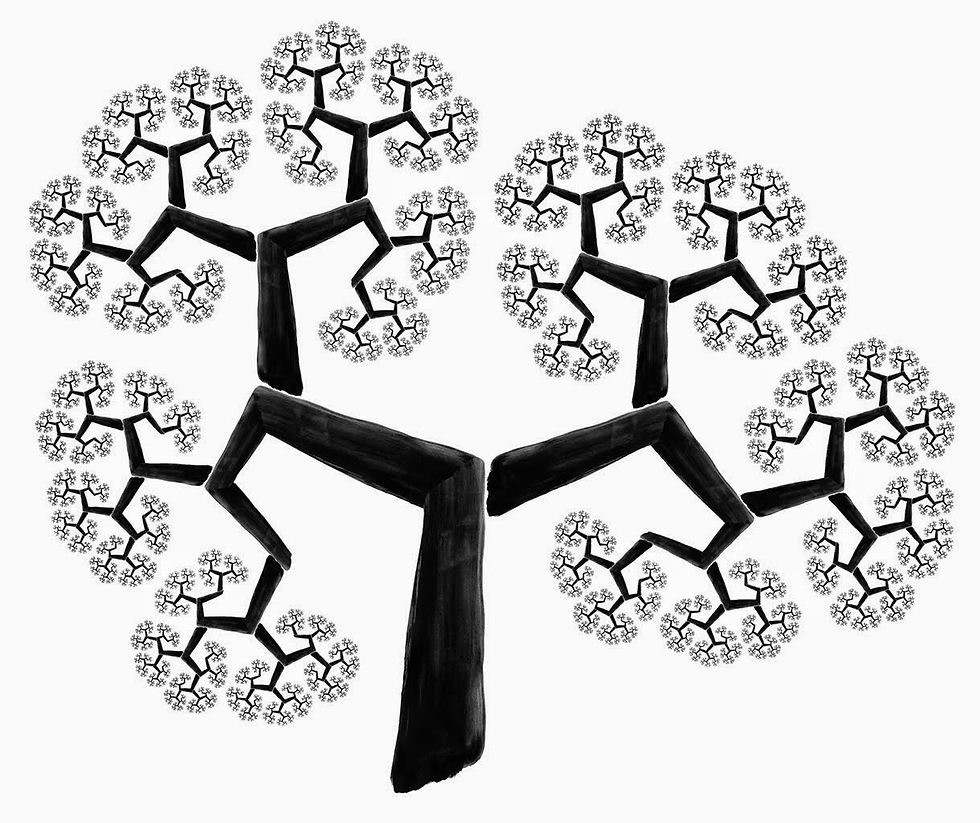
A árvore genealógica não é um fractal, pois não tem dimensão fracionária, no entanto, acrescentamos à árvore a característica do tamanho de seus galhos, diminuírem progressivamente à razão de um meio a cada iteração.



A árvore genealógica não é um fractal, pois não tem dimensão fracionária, no entanto, acrescentamos à árvore a característica do tamanho de seus galhos, diminuírem progressivamente à razão de um meio a cada iteração.
 Árvore Fractal.Construção do objeto matemático que representa a Àrvore Fractal. |  Curva de Koch.Construção do objeto que representa o Fractal do Floco de Neve de Koch. |
|---|---|
 I Feira Regional de Matemática.IFC/ Sombrio. |  I Feira Regional de Matemática.IFC/ Sombrio. |
 I Feira Regional de Matemática.IFC/ Sombrio. |  I Feira Regional de Matemática.IFC/ Sombrio. |
 I Feira Regional de Matemática.IFC/ Sombrio. |  I Feira Regional de Matemática.IFC/ Sombrio. |
 I Feira Regional de Matemática.IFC/ Sombrio. |  I Feira Regional de Matemática.IFC/ Sombrio. |
 I Feira Regional de Matemática.IFC/ Sombrio. |  Esperando o ônibus do IFC. |
 XXX Feira Catarinense de Matemática.Destino: Jaraguá do Sul |  XXX Feira Catarinense de Matemática.Destino: Jaraguá do Sul |
 XXX Feira Catarinense de Matemática.Jaraguá do Sul. |  Arena Jaraguá. |
 XXX Feira Catarinense de Matemática.Jaraguá do Sul. |  XXX Feira Catarinense de Matemática. |
 XXX Feira Catarinense de Matemática. |  XXX Feira Catarinense de Matemática. |
 XXX Feira Catarinense de Matemática. |  XXX Feira Catarinense de Matemática.Alunas Thays e Miriâ que representaram a turma na exposição e apresentação dos trabalhos. |
 XXX Feira Catarinense de Matemática. |  XXX Feira Catarinense de Matemática.Jaraguá do Sul. |
 XXX Feira Catarinense de Matemática. |  XXX Feira Catarinense de Matemática. |
 XXX Feira Catarinense de Matemática.Refeitório. |  XXX Feira Catarinense de Matemática.Cerimônia de abertura da premiação dos trabalhos. |
 XXX Feira Catarinense de Matemática.Premiação. |  XXX Feira Catarinense de Matemática.Jaraguá do Sul. |
 Representando a escola Dimer Pizzetti do município de Içara, dirigi-me ao gabinete do prefeito Murialdo Canto Gastaldon para apresentar nossa Menção Honrosa pela participação na Feira Catarinense. |
